Reversing the Bits of an Int
16 Jan 2012
The most efficient way to reverse an N bit integer on a PC is in O(lgN). This involves shifting registers by many places and not all architectures natively support that. Take AVR - LSL and LSR shift by 1 place only. Furthermore, many of the smaller AVR microcontrollers have limited memory space making look-up tables impractical. Fortunately, the naive linear bit reversal can be done in 2N operations, making it fast enough.
To reverse the bits in a register we need a stack - push the bit at one end, then shift the number towards the same end. After doing that for all bits we do the reverse: popping followed by shifts in the other direction. AVR and many other ISA allow this in hardware through the carry flag (CF).
.text
reverse_byte:
lsl r24 ; shift to the left, storing the high order bit in the CF
ror r25 ; rotate to the right, picking the high order bit from CF
lsl r24
ror r25
lsl r24
ror r25
lsl r24
ror r25
lsl r24
ror r25
lsl r24
ror r25
lsl r24
ror r25
lsl r24
ror r25
mov r24, r25 ; by calling convention the result must be in r24
ret
The need for bit reversal came when I wanted to do an efficient PWM (ignore for a bit that most AVR microcontrollers have hardware PWMs). A naive implementation is:
while(1)
if(counter++ < duty_cycle)
PORT = 1;
else
PORT = 0;
The problem is that we get consecutive strings of 1s or 0s and hence we need the iterations to be quick to make the flicker unnoticable (if driving LEDs for example). We can do better! How about the following?
while(1)
if(reverse_byte(counter++) < duty_cycle)
PORT = 1;
else
PORT = 0;
Reversing the bits in a byte is a peculiar operation: the transfer function is a rectangle in IO space!
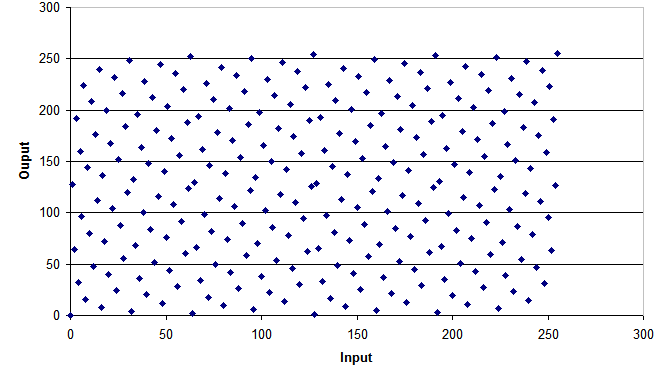
Transfer function of reverse_byte().
There seems to be some correlation between the sample locations, but overall there are no clusters and that's exactly what we wanted! Taking the average of 8 consecutive samples stays somewhat close around 128.
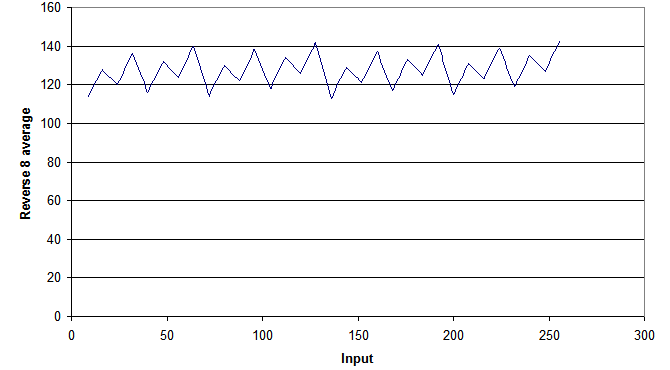
The same algorithm can be implemented for x86 (which is what I did to generate the plots) by replacing lsl and ror with their x86 equivalents: sal and rcr. Using inline assembly for MS VC++, we get:
unsigned int __declspec(naked) __fastcall reverse(unsigned int) {
__asm {
mov edx, ecx
mov ecx, 32
repeat:
sal edx, 1
rcr eax, 1
loop repeat
ret
}
}